数据结构小结
该文章主要用于存放数据结构思想和板子,具体做题思想以后补
挖坑:线段树专题、分块专题、平衡树专题
线段树
1.什么是线段树?
线段树本质就是一个二叉树,树上每个节点维护一段区间的值。
2.基本操作
建树(build)
- 就是从1号节点开始,每次劈两半,作为做儿子和右儿子,当发现当前结点的左右边界相等时,该节点的值即为建树序列的值。
查询(query)
- 递归查找,左边大于查找的左区间就查左儿子,右边同理。
修改(update)
- 如果修改区间覆盖当前区间,则直接给当前区间加上懒标记,否则递归查找加懒标记。
传递懒标记(push_down)
- 下传就完了。
3.代码:
Code
1 |
|
树状数组
1.什么是树状数组?
树状数组主要是利用二进制的性质来维护的数据结构,虽然不如线段树全能,但是比线段树简短,只不过思想可能难以理解。
2.如何维护?
每一个节点维护与其直连接点的和,具体可以看下面的图。
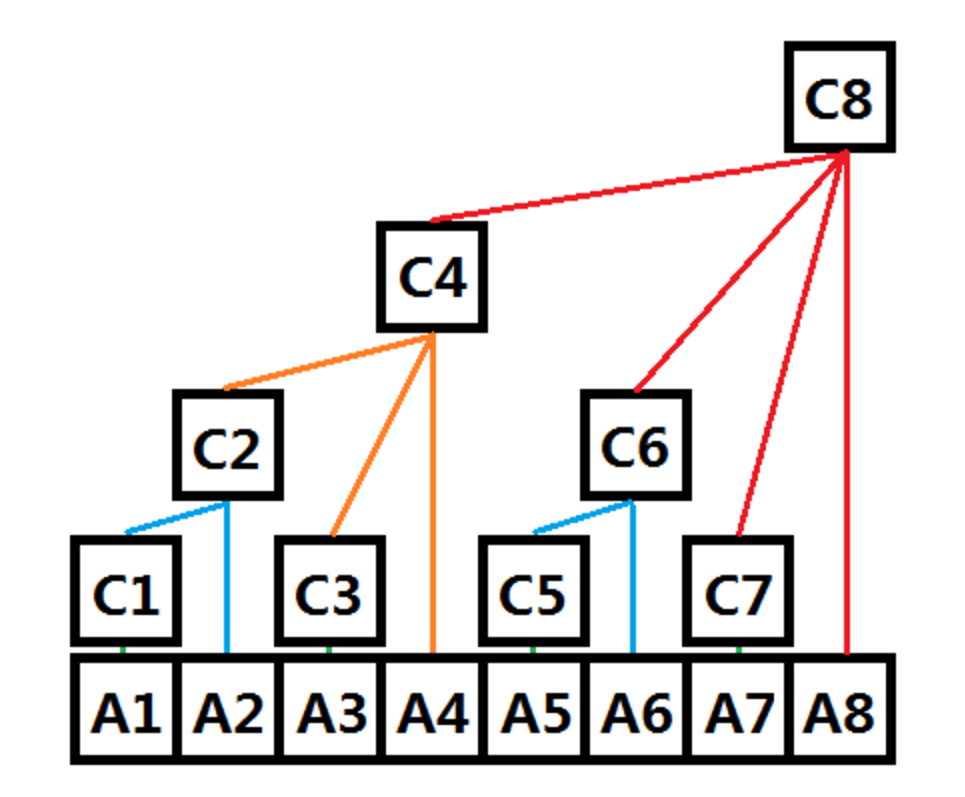
3.什么是lowbit?
lowbit就是找到一个数二进制下最后一个1。
代码:
lowbit(x)=x&(-x)
4.基本操作
单点修改(update)
从所选节点开始,增加自身及其父节点的值。
区间查询(query)
记录每个节点的前缀和,查询时用右范围的前缀和减去左范围。
5.代码:
Code
1 |
|
平衡树
1.什么是平衡树?
平衡树的出现是由于在某些情况下,二叉树的复杂度会因为重心的偏移而退化成
2.实现方法
因为平衡树的实现方法实在是太多了,没有办法(懒得)给大家展示,因此这里只给出Splay和FHQ的代码。
3.代码:
Splay
1 | template <class T> |
FHQ
1 |
|
分块
1.什么是分块?
分块就是将一个大序列分成好几个小块,如果修改范围覆盖一个块就给块打上标记,否则暴力修改。大部分情况下将快长设为
2.基本操作
初始化
处理出块长,然后
将各个点放在块内(说白了维护个数组,标记某个下表所在的块)。 区间修改、赋值(update)
和思想一样,遇到大块打标记,遇到零碎点暴力修改,复杂度
。 单点查询(ask)
看所在的块中有没有标记,有则下传,没有则直接输出。
3.代码:
Code
1 |
|
4.练习推荐
在 loj 上有 9道分块的专题训练 虽然数据很水,但是全部拿分块做下来之后会极大提高对分块的熟练度,十分推荐去做。
完结挖坑
[ ] 线段树题目讲解
[ ] 分块9题讲解
[ ] 平衡树题目讲解