1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
| #include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 200010;
int n, m;
vector<pair<int, int>> g[N];
void file()
{
#ifndef ONLINE_JUDGE
freopen("/workspaces/Code/test/test.in", "r", stdin);
freopen("/workspaces/Code/test/test.out", "w", stdout);
#endif
}
struct node
{
int name, dis;
node(int name = 0, int dis = 0) : name(name), dis(dis) {}
bool operator<(const node &a) const
{
return dis > a.dis;
}
};
const int inf = 0x3f3f3f3f;
int dis[N];
int dep[N];
int f[N][27];
void dj()
{
for (int i = 1; i <= n; i++)
dis[i] = inf;
dis[1] = 0;
priority_queue<pair<int,int>> q;
q.push(make_pair(0,1));
while (q.size())
{
int u = q.top().second;
q.pop();
for (int i = 0; i < g[u].size(); i++)
{
int v = g[u][i].first;
int w = g[u][i].second;
if (dis[v] > dis[u] + w)
{
f[v][0]=u;
dis[v] = dis[u] + w;
dep[v]=dep[u]+1;
q.push(make_pair(-dis[v],v));
}
}
}
}
void start() {
for(int i=1;i<=25;i++) {
for(int j=1;j<=n;j++) {
f[j][i]=f[f[j][i-1]][i-1];
}
}
}
int ans[N];
struct Node{
int u,v,val;
Node(int u=0,int v=0,int val=0) :u(u),v(v),val(val) {}
}no[N];
int nxt[N];
int top=0;
bool operator <(Node a,Node b) {
return dis[a.u]+dis[a.v] +a.val <dis[b.u]+dis[b.v]+b.val;
}
int check(int x) {
return (x==nxt[x])?x:(nxt[x]=check(nxt[x]));
}
signed main()
{
file();
scanf("%lld%lld",&n,&m);
for (int i = 1; i <= m; i++)
{
int u, v, val;
scanf("%lld%lld%lld",&u,&v,&val);
g[u].push_back({v, val});
g[v].push_back({u, val});
}
dj();
start();
for(int i=1;i<=n;i++) {
ans[i]=-1;
nxt[i]=i;
for(int j=0;j<g[i].size();j++) {
int u=i;
int v=g[i][j].first;
int w=g[i][j].second;
if(f[v][0]==u||f[u][0]==v||u>=v) continue;
no[++top]=Node(u,v,w);
}
}
sort(no+1,no+top+1);
for(int i=1;i<=top;i++) {
int u=no[i].u;
int v=no[i].v;
int val=no[i].val+dis[u]+dis[v];
int uf=check(u), vf=check(v);
while(uf!=vf){
if(dep[uf]<dep[vf]) swap(uf,vf);
ans[uf]=val-dis[uf];
nxt[uf]=f[uf][0];
uf=check(uf);
}
}
for(int i=2;i<=n;i++){
printf("%lld\n",ans[i]);
}
}
|
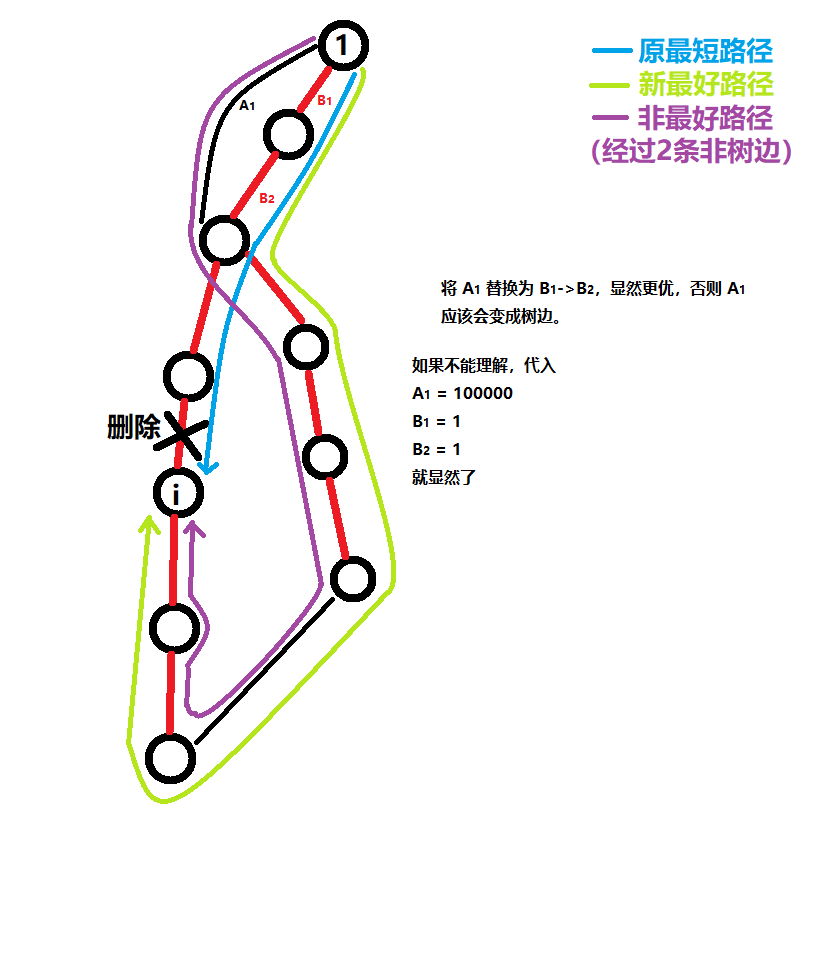
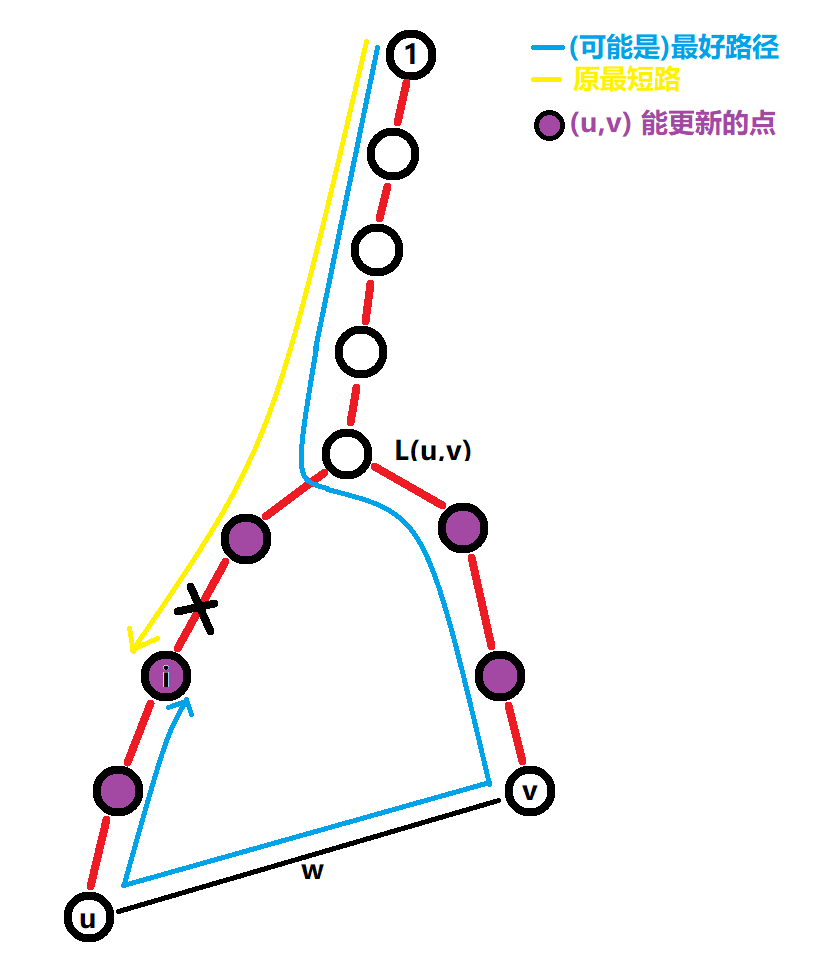
 我们看从1到6的最短路,应该是 1 -> 4 -> 6 ,如果跑次短路的话则会找到1 -> 2 -> 4 -> 6。诶,这不对吧,题目要求我们不经过1节点到i节点的最后一条边,也就是删去最短路上i节点的父边,但是这里并没有删,因此 次短路X。
我们看从1到6的最短路,应该是 1 -> 4 -> 6 ,如果跑次短路的话则会找到1 -> 2 -> 4 -> 6。诶,这不对吧,题目要求我们不经过1节点到i节点的最后一条边,也就是删去最短路上i节点的父边,但是这里并没有删,因此 次短路X。